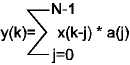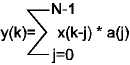Win FIR Filter Designer V2.5

Finite Impulse Response Filters

The N tap FIR filter consists of N-1 delayers, N multiplyers, each with its correspondant values a(j), and N-1 adders, or a global adder. The abbreviation FIR stands for Finite Impulse Response. Such is the characteristic of the impulse response of FIR filters. Because of the non-recurse filter structure, it is finite in duration. Actually it has a duration of N, where N is the number of taps of the filter.

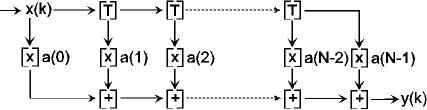
Figure 1: Structure of a FIR Filter

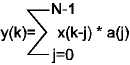
Figure 2: Convolution formula of a FIR Filter

One noticeable feature of FIR filters in general is their linear phase, because the delay is equal for all frequencies. This is especially important in video technology.

FIR Filter Design Principles

The problem of designing finite impulse response (FIR) digital filters experienced great activity in the early 1970`s. Most of this work was directed at the problem of optimal filter design, in the weighted Chebyshev sense. One algorithm for this program, by McClellan, Parks and Rabiner, will design the optimal Chebyshev approximation for linear phase filters. The Chebyshev optimization is done very efficiently by means of the Remez exchange algorithm, and this particular FIR filter design program has found wide use.
The filter design process is always a compromise among filter length, transition width and passband / stopband deviation (in the bandpass case). Not all of these specifications can be choosen arbitrarily.

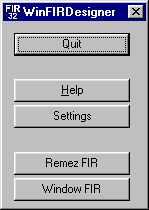
Figure 3: ScreenShot of FIR Filter Designer GUI

Equiripple FIR Filter Design

The method first programmed by Parks and McClellan in FORTRAN, uses an optimization algorithm called the Remez exchange algorithm. Instead of describing the coefficients by a Fourier series, they are described using a polynomial series. This design method allows sharper transitions with better stopband attenuation than the window method, but there is a ripple in the passband. This Remez type of design normally produces equiripple filters, where the ripples in the passbands and stopbands are of equal height within any one band.
The Remez algorithm also demands very high numerical precision, so the Win FIR Filter Designer V2.5 uses 64-bit double math precision arithmetic for all calculations. The program implements two slightly different variations of the algorithm.
The program provides the possibility to scale the calculated filter taps to a certain bitwidth. This is of particular interest for all people who want to implement their filter design on a DSP with integer arithmetic.

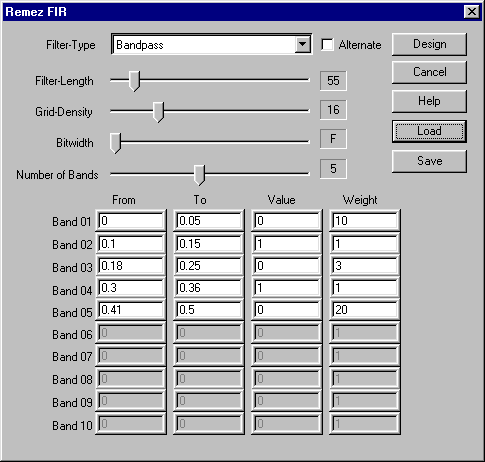
Figure 4: ScreenShot of Remez Design Method GUI

Window Method FIR Filter Design

The window method filter design process is based upon Fourier series. It is possible to represent a frequency function as a Fourier series, whose coefficients represent the coefficients of the filter.
To form a casual filter, the Fourier series is truncated and shifted. Truncating the Fourier series causes a phenomenon called the "Gibbs effect" - a spike occurs wherever there is a discontinuity in the desired magnitude of the filter. To counteract this, the filter coefficients are convolved in the frequency domain with the spectrum of a window function, thus smoothing the edge transitions at any discontinuity. This convolution in the frequency domain is equivalent to multiplying the filter coefficients with the window coefficients in the time domain.
The window design method starts with a very long series, in theory infinite, that is truncated to the desired length. Coefficients beyond the truncation are simply ignored. The window removes even more information. The equiripple method optimizes the series for a given number of coefficients.

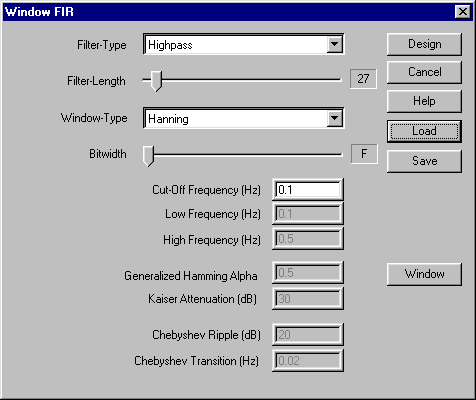
Figure 5: ScreenShot of Window Design Method GUI

Prism

The Win FIR Filter Designer V2.5 features a powerful data plotter module, called Prism, which displays the impulse response of the designed FIR filter in the frequency domain either as magnitude, phase, imaginary or real. The data can be scaled linear or logarithmic, both in the x-axis and in the y-axis. The filter taps are written to an external file, where they may be accessed by any third party program.

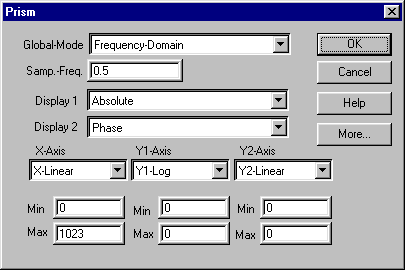
Figure 6: ScreenShot of Data Output Control Window

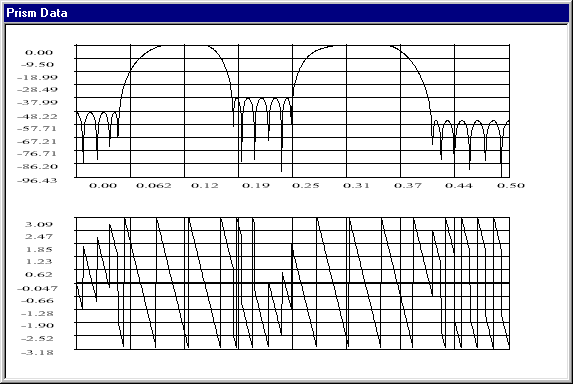
Figure 7: ScreenShot of Data Output Window

Download WinFIRDesigner V2.5 (174 KB)

Sources for FIR Design Algorithms